ルート２ルート２ルート２ルート２ルート…

http://www.hyuki.com/d/200706.html#i20070613102030 の

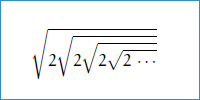
はいくつでしょう問題。
よし、現実逃避だ！やってみよう！
というわけで、

まじめに考える

$a_1=\sqrt{2}=2^{\frac{1}{2}}$ , $a_2=\sqrt{2a_1}=2^{\frac{1}{2}}{a_1}^{\frac{1}{2}}=2^{\frac{1}{2}}2^{{\frac{1}{2}}\cdot\frac{1}{2}}=2^{{\frac{1}{2}}+{\frac{1}{4}}}$ , $a_3=\sqrt{2a_2}=2^{\frac{1}{2}}{a_2}^{\frac{1}{2}}=2^{\frac{1}{2}}2^{({\frac{1}{2}}+{\frac{1}{4})\cdot\frac{1}{2}}}=2^{{\frac{1}{2}}+{\frac{1}{4}}+{\frac{1}{8}}}$ ,
なんで
$a_n=2^{\sum^{n}\frac{1}{2^n}}$
いえ〜い。
$\sum^{n}\frac{1}{2^n}$ は初項 $\frac{1}{2}$ 項比 $\frac{1}{2}$ の等比級数なので
$\sum^{\infty}\frac{1}{2^n}=\frac{\frac{1}{2}}{1-\frac{1}{2}}=1$
なので $\lim_{n\to\infty}a_n$ は 2 に収束っと。ほんとにあっているのかな。不安だ。

せっかく収束すると教えてくれているのだから

$\lim_{n\to\infty}a_n=x$ としたら $\lim_{n\to\infty}a_{n+1}=x$ でしょ。で、
$a_{n+1}=sqrt{2a_n}$
なので、
$x=sqrt{2x}$
いえ〜い。特性方程式〜（だっけ？）。だもんで
$x^2=2x$
$x=0,2$
と、いうわけで、0 はありえない（だって $a_{n-1}>0$ なら $a_n = \sqrt{2a_{n-1}} > 0$ に決まってるじゃない！）ので 2 に収束っと。大丈夫だよね。

絵的に考えると

$y=sqrt{2x}$ と $y=x$ の交点の y 座標だよねぃ。こうすると、さっき 0 が出てきたのも頷けるな。

検算

% ruby -e 'x=(ARGV[0] || 1).to_f; 50.times{puts x = Math.sqrt(2*x)}'

ちゃんと 2 に収束するよ！

ほんでもって、 x > 0 ならどんな x でも 2 に収束するよ！